Jumat, 25 Maret 2011

Limit Fungsi

Sebenernya saya sudah pernah menulis penjelasan definisi Limit tapi karena ada beberapa orang yang bilang penjelasan saya masih membingungkan. Okey, kali ini saya menjelas kan lagi mengenai limit dengan cara yang lebih sederhana.
{\displaystyle \lim_{x\rightarrow a}\, f(x)=L}
Didefinisikan sebagai berikut
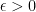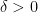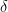untuk sebarang bilangan real \epsilon>0 (\epsilon dibaca epsilon) maka  terdapat bilangan real  \delta>0 (\delta dibaca delta) dimana 0<|x-a|<\delta yang berakibat  |f(x)-L|<\epsilon
atau dalam bahas simbol ditulis
(\forall\epsilon>0\;\exists\delta>0)\;0<|x-a|<\delta\Rightarrow|f(x)-L|<\epsilon
Apa maksud dari definisi tersebut? Apa maksud dari L adalah limit fungsi f di a. Nah sekarang perhatikan gambar


limit
Suatu fungsi f di a dikatakan mempunyai limit di L jika memenuhi hal-hal sebagai berikut
  1. Untuk sebarang bilangan real positif  \epsilon, saya katakan “sebarang” artinya kita bebas memilih bilangan real positif kita bisa memilih \epsilon=100000000 atau \epsilon=0.0000000001, terserah kita. Kemudian bentuk interfal I=\left(L-\epsilon,L+\epsilon\right) jelas L\in I. Interval I kita namakan himpunan persekitaran L
  2. Ada bilangan real postif \delta yang akan membentuk interfal A=\left(a-\delta,a+\delta\right) himpunan persekitaran a
  3. Untuk semua x\in A, x\neq a (dengan kata lain jarak x dengan a kurang dari \delta atau  |x-a|<\delta) yang berakibat f(x)\in I (dengan kata lain jarak f(x) dengan L kurang dari \epsilon atau |f(x)-L|<\epsilon)
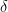Jadi untuk menunjukan L adalah limit fungsi f di c.  Pertama-tama bentuk interval I=\left(L-\epsilon,L+\epsilon\right) tidak peduli berapa panjang atau pendeknya interval tersebut. Apakah ada bilangan real postif \delta yang akan membentuk interval A=\left(a-\delta,a+\delta\right) yang memuat  x didalamnya (x\in A) sedemikian hingga f(x)\in I? Jika jawabannya ya, maka benar L adalah limit fungsi f di c.


Fisika XI



Dikutip dari: http://ade-tea.blogspot.com/2011/02/cara-membuat-widget-artikel-yang.html#ixzz1GwsyyEYg

Free Template Blogger collection template Hot Deals BERITA_wongANteng SEO theproperty-developer
Diposting oleh Colour of Life, dyy.. di 05.42
Label:

0 komentar:

Posting Komentar